Overview
Discover how the Mathematics Department nurtures confident problem-solvers through fun, discovery, and mastery at each level of primary school.
Overview
The Mathematics Department aims to nurture every ACSian into a passionate learner and a confident, creative problem-solver.
We strive to:
Create a dynamic and engaging learning environment that equips ACSians with the skills to apply Mathematics in real-life situations
Provide a holistic Mathematics programme across three key areas: Fun in Mathematics, Discovery in Mathematics, and Mastery in Mathematics
Inspire students to think critically, solve problems creatively, and develop a lifelong passion for Mathematics
FUN in MATHEMATICS (P1 and P2)
At the lower primary level, the focus is on cultivating joy in learning Mathematics. Students are engaged in hands-on activities, games, and basic heuristics to build foundational understanding. They are introduced to simple model drawing as a visual strategy to solve problems. These experiences aim to develop their confidence and curiosity from an early stage.
DISCOVERY in MATHEMATICS (P3 and P4)
In middle primary, students explore real-life applications of Mathematics to discover its relevance and meaning in the world around them. Games continue to be used to reinforce learning in a fun and interactive way. Students who demonstrate strong aptitude and interest in Mathematics may be selected to join the Thoburn Programme, where they delve deeper into Mathematical concepts through problem investigation and interdisciplinary connections.
MASTERY in MATHEMATICS (P5 and P6)
At the upper primary level, the emphasis shifts towards consolidation and mastery of key Mathematical concepts. Students are challenged to apply their learning in more complex contexts. Those with a strong aptitude for Mathematics can further stretch their potential through the Math Olympiad and Thoburn programmes. Students who benefit from additional support are placed in the Mathematics Foundation Programme, where they receive targeted instruction tailored to their learning needs and pace.
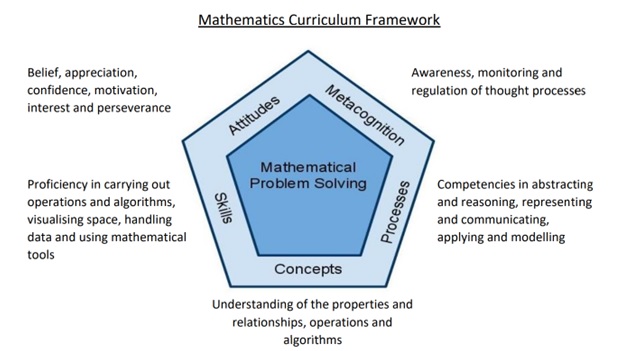
Mathematics Framework
The central focus of the mathematics curriculum is the development of mathematical problem-solving competency. Supporting this focus are five inter-related components – concepts, skills, processes, metacognition and attitudes.
